cdoku - a sudoku solver built in C

What is cdoku?

Cdoku is a sudoku solver that - you guessed it - is built in C.

It can take an input of a 9x9 sudoku grid as formatted below in a CSV file and output the result in a formatted table, for example:

Input:

.,.,.,.,.,.,.,.,.
.,.,.,.,7,6,.,2,.
.,.,4,8,.,.,1,.,.
.,.,5,9,4,.,8,.,.
.,.,.,7,.,.,.,5,.
.,9,6,.,.,.,.,7,2
8,.,.,5,.,4,.,.,7
.,.,.,.,3,.,2,.,.
1,4,.,.,.,.,.,.,.

Output:

|6|2|8|3|5|1|7|9|4|
|3|1|9|4|7|6|5|2|8|
|5|7|4|8|2|9|1|6|3|
|7|3|5|9|4|2|8|1|6|
|2|8|1|7|6|3|4|5|9|
|4|9|6|1|8|5|3|7|2|
|8|6|2|5|1|4|9|3|7|
|9|5|7|6|3|8|2|4|1|
|1|4|3|2|9|7|6|8|5|

I originally created this as a way to get back into doing more C programming as I hadn’t done it for a few years. Writing a sudoku solver is also a great refresh of solving a backtracking problem.

Approach

As mentioned, solving a sudoku puzzle fits a backtracking problem. This means that we have the three things we need to figure out:

1. Choices
2. Our constraints
3. A goal

Choices: The choices we have here are choosing a character between 1 and 9, as these are the valid values for a sudoku board.

Constraints: The constraints we have are the standard rules of sudoku, meaning that:

1. A number can only occur once in a column
2. A number can only occur once in a row
3. A number can only occur once in an inner box (a 3x3 box in this case)

Goal: As we make choices, we will fill in each cell, converging on a completed board, so our goal here is to fill the board.

Implementation

I’ve included a copy of my solution in a github repo here if you wan’t to follow along.

The implementation imports the grid from a file, which I won’t cover here as I’m focusing on the approach instead.

After importing the board, the first step to get started is to ‘solve’ the board for our initial index, which in this case is 0,0. We only need this single call to solve the entire board as inside the solveForIndex we will call this function again for the following indexes, as 0,0.

Validation, base cases and our goal.

The first thing we do in the solveForIndex function is check a few things:

if (row == BOARD_HEIGHT){
    return true;
}

// If the col is the max width,
// move on to the next row.
if (col == BOARD_WIDTH){
    return solveForIndex(board, row + 1, 0);
}

char existingChar = board[row][col];

if (existingChar != '.'){
    return solveForIndex(board, row, col + 1);
}

1. We check to see if we have just completed the last row of the puzzle, and are now on the next row. We can return true here as we know we have just solved the puzzle. This is our goal from earlier.

2. The next thing we can check is that have we just finished the last column in a row. If we have, we can call the solveForIndex again, starting on the next row, back in column 0. These first two checks act as our base case for our recursive function.

3. We can also retrieve the existing char in this cell here, and see if it isn’t equal to the . char. This is because we use the . char as a placeholder to say we need to solve that cell. We also need to skip over these cells that already have a value as these will be part of the initial puzzle.

After doing these checks, we can then move on to actually solving the solution.

Checking validity

The next part we can complete is to start choosing values and putting them into our grid to see if we can solve the grid using that value. This is where we use our choices from the introduction above

for(char currChoice = '1'; currChoice <= '9'; currChoice++){
    // If the board is valid with this char at this index
    bool isValid = isValidBoard(board, row, col, currChoice);
    if (isValid) {
        board[row][col] = currChoice;

        // If we can complete the puzzle from here with this move, return true;
        bool canComplete = solveForIndex(board, row, col + 1);
        if (canComplete){
            return true;
        } else {
            // Otherwise reset
            board[row][col] = '.';
        }
    }
}
return false;

This code will loop through all of the 9 possible choices for this cell from 1-9. After making our choice, the first thing we need to check is that if we can use the choice and still have a valid board.

This is where we need to use our constraints from earlier.

Constraints - Determining if we have a valid board.

To determine if the board is valid with our choice, I created this function: isValidBoard:

/**
 * Identifies if the board with a choice of this char is valid
 * @param board Board array
 * @param row Possible row
 * @param column Possible column
 * @param choice Choice of character
 */
bool isValidBoard(char** board, int row, int column, char choice){
    /*
     * What makes a board valid in sudoku?
     * Need to check against the row
     * - There cannot be another one of the char in a row
     * Need to check against the column
     * - There cannot be another one of the char in the column
     * Need to check the grid
     * - There cannot be another one of the char in the grid (currently 3x3 as working on 9x9 grid)
     * - Can be worked out by sqrt (width) or sqrt (height) as grid will be square - currently using const
     */

    bool validRow = isValidRow(board, row, choice);
    if (!validRow){
        return false;
    }

    bool validColumn = isValidColumn(board, column, choice);
    if (!validColumn){
        return false;
    }

    bool validSquare = isValidSquare(board, row, column, choice);
    if (!validSquare){
        return false;
    }

    return true;
}

This function breaks down into three smaller functions to check the boards properties.

Checking if the row is valid

To check if the row is valid, all we need to do is check all of the entries in the given row to see if our choice already exists in this row. We can do this with the following code which check each index in the row:

/**
 * Checks if the choice can be used in the current row.
 * @param board array of array of chars.
 * @param row row to check
 * @param choice current choice
 * @return true if valid, false if not
 */
bool isValidRow(char** board, int row, char choice){
    char* boardRow = board[row];
    for (int i = 0; i < BOARD_WIDTH; ++i) {
        char currEntry = boardRow[i];
        if (currEntry == choice) {
            return false;
        }
    }
    return true;
}

Checking if a column is valid

This is very similar to the function for seeing if a row is valid, except for we look into each value in the column instead of a row. We can do this using the following:

/**
 * Checks if the choice can be used in a row
 * @param board array of array of  chars
 * @param column column to check
 * @param choice choice to test
 * @return true if valid, false if not
 */
bool isValidColumn(char** board, int column, char choice){
    for (int row = 0; row < BOARD_HEIGHT; ++row) {
        char currEntry = board[row][column];
        if (currEntry == choice){
            return false;
        }
    }
    return true;
}

Checking if a sub-square is valid

Checking if one of the squares inside the sudoku grid is slightly more complicated than the previous two checks as we also need to check multiple rows / columns.

We can do this by first identifying the initial row / column of the square, which we can do by dividing it by the width / height of one of these sub-grids (which is 3 as we are using a 9x9 grid), and then multiplying it again by the width.

We can then just iterate through both the width and the row / column indexes until we reach the next grid, which will be the initial row / column + the grid width. This is then similar to the row / column checks as all we then need to do is see if we find the same value as our choice.

/**
 * Determines if the choice can be placed into the square
 * @param board Array of array of chars
 * @param row row to check
 * @param column column to check
 * @param choice choice to test
 * @return true if valid, false if not
 */
bool isValidSquare(char** board, int row, int column, char choice) {
    int initialRow = (row / GRID_WIDTH) * GRID_WIDTH;
    int initialColumn = (column / GRID_WIDTH) * GRID_WIDTH;

    for(int i = initialRow; i < initialRow + GRID_WIDTH; ++i){
        for (int j = initialColumn; j < initialColumn + GRID_WIDTH; ++j) {
            char currChar = board[i][j];
            if(currChar == choice)
            {
                return false;
            }
        }
    }
    return true;
}

Putting our choice into the board and moving on to the next cell.

Now we know we can put our choice into the board, and see if we can solve it from here:

for(char currChoice = '1'; currChoice <= '9'; currChoice++){
    // If the board is valid with this char at this index
    bool isValid = isValidBoard(board, row, col, currChoice);
    if (isValid) {
        board[row][col] = currChoice;

        // If we can complete the puzzle from here with this move, return true;
        bool canComplete = solveForIndex(board, row, col + 1);
        if (canComplete){
            return true;
        } else {
            // Otherwise reset
            board[row][col] = '.';
        }
    }
}
return false;

The first thing we can do is update the board by getting a copy of the row, updating it to include the new value and then replacing the row in the board.

We this, we then call our solveForIndex method again, passing in the next column. We don’t need to worry about if this is a valid column / on the board, as our checks at the start of the function will handle this.

If we can complete the board with this choice, which we will get as true if we can get to the end of the board with our current choice, we can also return true from our current call to this function.

If we can’t complete the board, we need to reset our choice back to be our placeholder ..

If we go through all of our choices here and we can’t solve the board, we will also return false, as one of our previous choices has not been correct. This is where we do our backtracking, as we will go back out to where we made our choice.

Assumptions

Our approach makes the following solutions:

1. We are given a board that is solvable.
2. Our width and height dimensions of the grid are the same.

Going further and improving our solution

Handling an invalid puzzle

The first way we could improve our solution is to handle invalid puzzles. We could do this by checking the return value of the solveForIndex method in the main function and only printing out the result of the solver when the function returns true.

Handling puzzles of different sizes

We could also handle puzzles of different sizes. This should have two much of an impact on the program as it would mainly involve updating the constants used when checking a row / column / sub-square is valid. We could, for example, allow the user to pass these in as arguments to the program.

Fixing memory leaks

The current solution does try to free the memory used by the board after it has been used, however, after running valgrind, there still seems to be a block that is still being used when the program exists, as can be seen below.

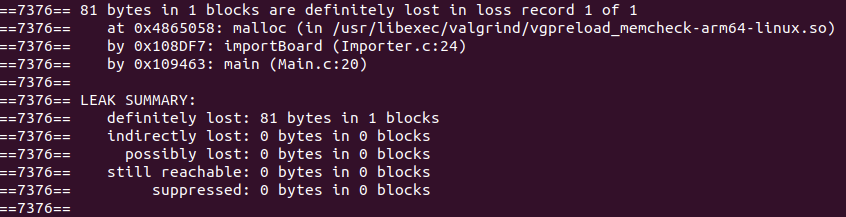
There will likely be a better way to initialize the array in the first place which may help, but it’ll be interesting to look into, especially after not having done any C programming for a while!

Summary

Having now looked at this as an example of using backtracking to solve a problem like this, I’m planning on writing a few more posts that look into how to solve these interview style questions which will hopefully be useful.

If you want to take a bit of a deeper dive into the solution, I’ve created a github repo for it here.

If you’re interested in seeing more of these sorts of problems and breakdowns of how to solve them, I’d highly recommend you check out Back To Back SWE on youtube as they cover loads of problems like this and go in to a lot of detail solving them.